Advanced guides on electron integral
Computing the electron integrals is a crucial part of quantum chemistry, especially for the generation of molecular Hamiltonians. In previous tutorials, we explained how to obtain electron integrals (eInts) as well as the molecular Hamiltonian. In this tutorial, we give more detailed introductions on objects that QURI Parts provides for computing eInts, so that you may customize your algorithms for efficient eInt computations.
The standard steps of computing the electron integrals (eInts) involve:
- Obtain AO eInts from the molecule.
- Run self-consistent computation.
- Obtain spatial MO eInts from AO eInts and RHF.
- Convert spatial MO eInts to spin MO eInts.
As there are multiple types of electron integrals involved in the computation, and it is usually the case that we only need the spin MO eInt, QURI Parts provide 2 ways of obtaining the spin MO eInt.
- Save all the intermediate eInts on memory.
- Release the eInt array to the memory on demand.
We will present how to do the two versions of computations in this tutorial.
Overview
Here we give a brief introduction of how to perform the two versions of computation.
Quick summary: Compute with storing the electron integral arrays on memory
1. Define the molecule
from pyscf import gto, scf
from quri_parts.pyscf.mol import PySCFMolecularOrbitals, get_ao_eint_set
mole = gto.M(atom="O 0 0 0; H 0.2774 0.8929 0.2544; H 0.6068, -0.2383, -0.7169")
mf = scf.RHF(mole).run(verbose=0)
mo = PySCFMolecularOrbitals(mole, mf.mo_coeff)
2. Compute the AO eInts
ao_eint_set = get_ao_eint_set(mo, store_array_on_memory=True)
3. Compute the spin MO eInts
spin_mo_eint_set = ao_eint_set.to_full_space_mo_int(mo)
h2o_const = spin_mo_eint_set.const
h2o_1e_int = spin_mo_eint_set.mo_1e_int.array
h2o_2e_int = spin_mo_eint_set.mo_2e_int.array
4. Compute the active space spin MO eInts
from quri_parts.chem.mol import ActiveSpaceMolecularOrbitals, cas
# Define the active space
active_space = cas(n_active_ele=6, n_active_orb=4)
asmo = ActiveSpaceMolecularOrbitals(mo, active_space)
# Compute the active space MO integrals
cas_spin_mo_eint_set = ao_eint_set.to_active_space_mo_int(asmo)
h2o_cas_const = cas_spin_mo_eint_set.const
h2o_cas_1e_int = cas_spin_mo_eint_set.mo_1e_int.array
h2o_cas_2e_int = cas_spin_mo_eint_set.mo_2e_int.array
Quick summary: Compute without storing the electron integral arrays on memory
1. Define the molecule
from pyscf import gto, scf
from quri_parts.pyscf.mol import PySCFMolecularOrbitals, get_ao_eint_set
mole = gto.M(atom="O 0 0 0; H 0.2774 0.8929 0.2544; H 0.6068, -0.2383, -0.7169")
mf = scf.RHF(mole).run(verbose=0)
mo = PySCFMolecularOrbitals(mole, mf.mo_coeff)
2. Compute the AO eInts
ao_eint_set = get_ao_eint_set(mo)
3. Compute the spin MO eInts
spin_mo_eint_set = ao_eint_set.to_full_space_mo_int(mo)
# nuclear repulsion
h2o_const = spin_mo_eint_set.const
# 1-electron eInt array
h2o_1e_int = spin_mo_eint_set.mo_1e_int.array
# 2-electron eInt array
h2o_2e_int = spin_mo_eint_set.mo_2e_int.array
4. Compute the active space spin MO eInts
# Define the active space
active_space = cas(n_active_ele=6, n_active_orb=4)
asmo = ActiveSpaceMolecularOrbitals(mo, active_space)
# Compute the active space MO integrals
cas_spin_mo_eint_set = ao_eint_set.to_active_space_mo_int(asmo)
# active space nuclear repulsion
h2o_cas_const = cas_spin_mo_eint_set.const
# active space 1-electron eInt array
h2o_cas_1e_int = cas_spin_mo_eint_set.mo_1e_int.array
# active space21-electron eInt array
h2o_cas_2e_int = cas_spin_mo_eint_set.mo_2e_int.array
Quick comment
The two computations above looks almost the same. The only difference is in get_ao_eint_set, where one sets the store_array_on_memory argument to True. However, they behave very differently under the hood.
In the first version where the store_array_on_memory = True, the AO electron integrals are released to the memory right after get_ao_eint_set, ao_eint_set.to_full_space_mo_int and ao_eint_set.to_active_space_mo_int are executed. This takes up more memory but can provide potential speed advantage. We will discuss how to compute electron integrals in the shortest amount of time in later sections.
For the second version where we use the default store_array_on_memory = False, the explicit eInt array are released to memory only when the .array property is called. This saves up a lot of memory during actual computations and has more advantages when we are considering larger molecules. In the Hamiltonian generation tutorial, the get_spin_mo_integrals_from_mole runs this version of computation.
The electron integral interface
As there are multiple kinds of electron integrals, this section is devoted to explain how they are represented in QURI Parts.
There are 3 types of electron integrals, and each of them can be divided into constant part, 1-electron integral and 2-electron integrals.
- Atomic orbital (AO) electron integrals (
AOeIntSet):- constant: nuclear repulsion
AO1eInt: 1-electron AO integral.AO2eInt: 2-electron AO integral.
- Spatial molecular orbital (MO) electron integrals (
SpatialMOeIntSet):- constant: nuclear repulsion
SpatialMO1eInt: 1-electron spatial MO integralSpatialMO2eInt: 2-electron spatial MO integral
- Spin molecular orbital (MO) electron integrals (
SpinMOeIntSet):- constant: nuclear repulsion
SpinMO1eInt: 1-electron spatial MO integralSpinMO2eInt: 2-electron spatial MO integral
All the ...1eInt and ...2eInt objects provide .array property that allows us to retrieve the explicit electron integral represented by a Numpy array.
In QURI Parts, the relations between the electron integral sets are represented by the following diagram.
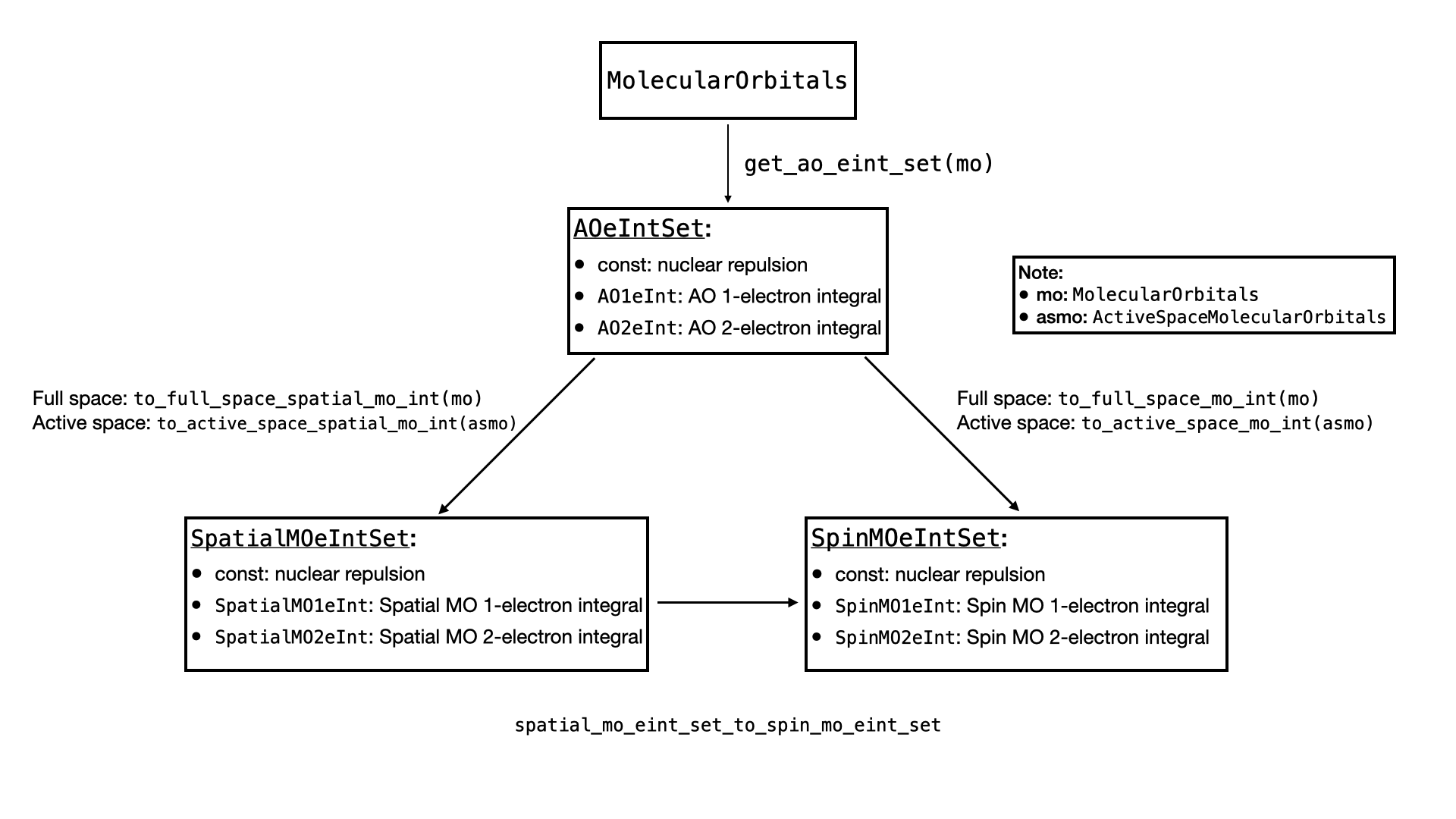
Compute the Electron Integrals
Here, we introduce the first way of computing the electron integrals, where we release all the electron integrals of each intermediate step onto the memory. We first list out all the objects that represents an electron integral:
- AO electron integral:
AOeIntArraySet, which contains:- constant: The nuclear repulsion energy.
AO1eIntArray: The AO 1-electron integral array on memoryAO2eIntArray: The AO 2-electron integral array on memory
- Spatial electron integral:
SpatialMOeIntSet, which contains:- constant: The nuclear repulsion energy.
SpatialMO1eIntArray: The spatial MO 1-electron integral array on memorySpatialMO2eIntArray: The spatial MO 2-electron integral array on memory
- Spin electron integral:
SpinMOeIntSet, which contains:- constant: The nuclear repulsion energy.
SpinMO1eIntArray: The spin MO 1-electron integral array on memorySpinMO2eIntArray: The spin MO 2-electron integral array on memory
Computing the AO electron integrals
One can construct the AOeIntArraySet using the get_ao_eint_set function. When the store_array_on_memory argument is set to True, it returns an AOeIntArraySet object that stores the AO electron integrals on memory.
from quri_parts.pyscf.mol import get_ao_eint_set
ao_eint_set= get_ao_eint_set(mo, store_array_on_memory=True)
# the nuclear repulsion energy
nuc_energy= ao_eint_set.constant
# the AO one-electron integrals: an AO1eIntArray object
ao_1e_int= ao_eint_set.ao_1e_int
# the AO two-electron integrals: an AO2eIntArray object
ao_2e_int= ao_eint_set.ao_2e_int
One can access the explicit array of the electron atomic orbital integrals with the array attribute:
# ao_1e_int.array
# ao_2e_int.array
Computing the spatial and spin MO electron integrals
With the AO electron integrals and the MolecularOrbitals at hand, we may compute the:
- spatial MO electron integrals with the
to_full_space_spatial_mo_intmethod - spin MO electron integrals with the
to_full_space_mo_intmethods
in ao_eint_set. Note that the explicit array of the integrals are computed and released to the memory once these methods are called.
# Computes the full space spatial mo electron integrals
spatial_mo_e_int_set = ao_eint_set.to_full_space_spatial_mo_int(mo)
# Computes the full space spin mo electron integrals
spin_mo_e_int_set = ao_eint_set.to_full_space_mo_int(mo)
To access the explicit array of the integrals, you may run:
# For the spatial MO electron integrals
nuclear_repulsion_energy = spatial_mo_e_int_set.const
spatial_1e_int = spatial_mo_e_int_set.mo_1e_int.array
spatial_2e_int = spatial_mo_e_int_set.mo_2e_int.array
# For the spin MO electron integrals
nuclear_repulsion_energy = spin_mo_e_int_set.const
spin_1e_int = spin_mo_e_int_set.mo_1e_int.array
spin_2e_int = spin_mo_e_int_set.mo_2e_int.array
Computing the active space electron integrals
The active space spin and spatial MO eInts can also be computed in a similar way. Instead of using the full space MolecularOrbitals, we compute the:
- active space spatial MO eInt with the
to_active_space_spatial_mo_intmethod - active space spin MO eInt with the
to_active_space_mo_intmethod
by passing in the ActiveSpaceMolecularOrbitals. Note that the explicit eInt arrays are released onto the memory once these methods are called.
# Computing the active space spatial mo electron integrals
active_space_spatial_integrals = ao_eint_set.to_active_space_spatial_mo_int(active_space_mo=asmo)
# Computing the active space spin mo electron integrals
active_space_spin_integrals = ao_eint_set.to_active_space_mo_int(active_space_mo=asmo)
To obtain the explicit active space MO eInts
# For the spatial MO electron integrals
active_space_nuclear_repulsion_energy = active_space_spatial_integrals.const
active_space_spatial_1e_int = active_space_spatial_integrals.mo_1e_int.array
active_space_spatial_2e_int = active_space_spatial_integrals.mo_2e_int.array
# For the spin MO electron integrals
active_space_nuclear_repulsion_energy = active_space_spin_integrals.const
active_space_spin_1e_int = active_space_spin_integrals.mo_1e_int.array
active_space_spin_2e_int = active_space_spin_integrals.mo_2e_int.array
Computing active space eInt with optimal efficiency
To achieve optimal efficiency when computing active space eInts, we recommend using the
get_active_space_spatial_integrals_from_mo_eintget_active_space_spin_integrals_from_mo_eint
functions as the to_active_space_spatial_mo_int and to_active_space_mo_int methods computes the full space MO eInt first before projecting them onto the selected active space. This does not matter if one wants to compute eInts for only one active space configuration. However, the MO eInts are calculated repeatedly if multiple active space eInts are required and can cause performance penalty. Thus, it is more efficient if we compute the MO eInt once and store it on memory and then project the eInts to the desired active spaces with the aforementioned functions:
from quri_parts.chem.mol import (
get_active_space_spatial_integrals_from_mo_eint,
get_active_space_spin_integrals_from_mo_eint
)
# Computing the active space spatial mo electron integrals
active_space_spatial_integrals = get_active_space_spatial_integrals_from_mo_eint(
active_space_mo=asmo, electron_mo_ints=spatial_mo_e_int_set
)
# Computing the active space spin mo electron integrals
active_space_spin_integrals = get_active_space_spin_integrals_from_mo_eint(
active_space_mo=asmo, electron_mo_ints=spatial_mo_e_int_set
)
Compute the electron integrals in a memory efficient manner
When the molecule gets larger, it is unrealistic to store the full space mo electron integrals on memory, most especially when we just want to get the eInts of a small active space from a big molecule. In QURI Parts, we provide a memory efficient way of computing the active space integrals while bypassing the full space electron integrals. The idea is to store only the PySCF Mole object and the mo coefficients on memory. The explicit eInts are only released onto the memory on demand.
We first introduce the objects used to perform memory efficient eInt evaluation
- AO electron integral:
PySCFAOeIntSet, which contains:- constant: The nuclear repulsion energy.
PySCFAO1eInt: The AO 1-electron integral.PySCFAO2eInt: The AO 2-electron integral.
- Full space spatial electron integral:
SpatialMOeIntSet, which contains:- constant: The nuclear repulsion energy.
PySCFSpatialMO1eInt: The spatial MO 1-electron integral.PySCFSpatialMO2eInt: The spatial MO 2-electron integral.
- Full space spin electron integral:
SpinMOeIntSet, which contains:- constant: The nuclear repulsion energy.
PySCFSpinMO1eInt: The spin MO 1-electron integral.PySCFSpinMO2eInt: The spin MO 2-electron integral.
The above objects only holds the Molecule objects and the mo coefficients. The actual eInt array are only computed when the .array property is accessed. For the active space MO eInts, they are stored by:
- Active space spatial electron integral:
SpatialMOeIntSet, which contains:- constant: The nuclear repulsion energy.
SpatialMO1eIntArray: The spatial MO 1-electron integral.SpatialMO2eIntArray: The spatial MO 2-electron integral.
- Active space spin electron integral:
SpinMOeIntSet, which contains:- constant: The nuclear repulsion energy.
SpinMO1eIntArray: The spin MO 1-electron integral.SpinMO2eIntArray: The spin MO 2-electron integral.
where the explicit array are released to the memory once the PySCFAOeIntSet.to_active_space_mo_int or PySCFAOeIntSet.to_active_space_spatial_mo_int is called.
Computing the AO spatial electron integrals
We may obtain the PySCFAOeIntSet using the get_ao_eint_set function with the store_array_on_memory option to False
# This constructs a PySCFAOeIntSet object, which only holds pyscf mol object on memory
pyscf_ao_eint_set = get_ao_eint_set(
mo,
store_array_on_memory=False # default to False
)
Computing the spatial and spin MO electron integrals
As in the AOeIntArraySet, the full space spatial and spin MO eInts can be calculated by the to_full_space_spatial_mo_int and to_full_space_mo_int respectively.
# Returns a SpatialMOeIntSet object, which only holds the molecule and the mo coefficients on memory
pyscf_spatial_mo_eint_set = pyscf_ao_eint_set.to_full_space_spatial_mo_int(mo)
# Returns a SpinMOeIntSet object, which only holds the molecule and the mo coefficients on memory
pyscf_spin_mo_eint_set = pyscf_ao_eint_set.to_full_space_mo_int(mo)
The explicit electron integrals are only computed on demand when the array property is accessed
# For the spatial MO electron integrals
pyscf_nuclear_repulsion_energy = pyscf_spatial_mo_eint_set.const
pyscf_spatial_1e_int = pyscf_spatial_mo_eint_set.mo_1e_int.array # computation happens here
pyscf_spatial_2e_int = pyscf_spatial_mo_eint_set.mo_2e_int.array # computation happens here
# For the spin MO electron integrals
pyscf_nuclear_repulsion_energy = pyscf_spin_mo_eint_set.const
pyscf_spin_1e_int = pyscf_spin_mo_eint_set.mo_1e_int.array # computation happens here
pyscf_spin_2e_int = pyscf_spin_mo_eint_set.mo_2e_int.array # computation happens here
Getting the active space spin electron integrals
We may also compute the:
- active space spatial MO eInt with the
PySCFAOeIntSet.to_active_space_spatial_mo_intmethod - active space spin MO eInt with the
PySCFAOeIntSet.to_active_space_mo_intmethod
just like how we computed them with the AOeIntArraySet. Note that the computation is performed with pyscf’s CASCI once these methods are called.
# Computing the active space spatial mo electron integrals
pyscf_active_space_spatial_integrals = pyscf_ao_eint_set.to_active_space_spatial_mo_int(asmo)
# Computing the active space spin mo electron integrals
pyscf_active_space_spin_integrals = pyscf_ao_eint_set.to_active_space_mo_int(asmo)